Pso Summary

粒子群最適化（PSO）

1. 粒子群最適化 (PSO) の概要と学術的背景

1.1 PSOの定義と起源

粒子群最適化（Particle Swarm Optimization, PSO）は, 1995年にJames KennedyとRussell Eberhartによって開発された, 群知能に基づく強力な最適化手法です. その学術的な基盤は, 彼らが発表した研究論文に明確に記されており, この分野における重要な出発点となっています. このアルゴリズムは, 自然界の生物, 特に鳥の群れが餌を探す行動や魚の群れが集団で移動する行動から着想を得ています.

魚の群れ

鳥の群れ

PSOの根幹にある考え方は, 「情報を群れ全体で共有する」という点にあります. 群れを構成する個体（粒子）が, それぞれがこれまでに発見した最も優れた位置pbest（パーソナルベスト）と, 群れ全体で発見された最も優れた位置gbest（グローバルベスト）の情報を共有し, それらを参考にしながら探索空間を移動することで, 良好な解へと収束していきます. この情報共有の仕組みが, PSOの探索効率を高める上で極めて重要です.

PSOは, 目的関数の情報が明示的に与えられていないブラックボックス最適化問題に対しても効果的な解法の一つとして位置づけられ, 勾配情報が利用できない, あるいは計算が困難な場合に特にその有用性が発揮されます.

PSOの概念を理解する上で, 自然界の振る舞いからの着想は非常に有効な導入となります. この生物学的アナロジーは, アルゴリズムの直感的な理解を促し, 複雑な数学的モデルの背景にあるシンプルなアイデアを把握しやすくします. このような直感的な導入は, 学術的な厳密さを保ちつつも, より幅広い層の学習者がPSOの基本的な概念にアクセスしやすくなるという利点をもたらします. この特性は, PSOが学術研究だけでなく, 実用的な応用においても広く普及する一因となっています.

1.2 群知能としてのPSOの位置づけ

PSOは, アリコロニー最適化（ACO）などと共に, 「群知能最適化（Swarm Intelligence Optimization）」という計算パラダイムに属します. 群知能とは, 個々のエージェントが単純なルールに従いながらも, 相互作用を通じて群れ全体として複雑で知的な行動を示す現象をモデル化するアプローチです. このアプローチは, 情報が分散していて常に変化し続けている実世界での問題, 例えばインターネットにおけるルーティング最適化やマルチエージェントシステムにおける協調行動などへの応用が期待されています.

群知能最適化の文脈では, 「探索（exploration）」と「開拓（exploitation）」のバランスが極めて重要です. 探索は解空間の未踏領域を広範囲に調査する能力を指し, 開拓は既に見つかった有望な解の近傍を詳細に調べる能力を指します. PSOは, 個体自身の最良経験（自己認識）と群れ全体の最良経験（社会認識）を組み合わせることで, この探索と開拓のバランスを効果的に実現します.

2. 粒子群最適化 (PSO) の基礎理論とアルゴリズム

2.1 PSOの概念と自然界からの着想

PSOは, 鳥の群れが餌を探す行動や魚の群れが捕食者から逃れる行動に見られる, 集団としての効率的な探索戦略をモデルにしています. 個々の鳥（粒子）は, 自身の経験（最も良い餌場）と, 群れ全体の情報（群れの中で最も良い餌場）を共有し, これらに基づいて次の行動を決定します. この集団行動の模倣により, 個々の粒子は局所的な探索と大域的な探索のバランスを取りながら, 効率的に良い解へと収束していきます.

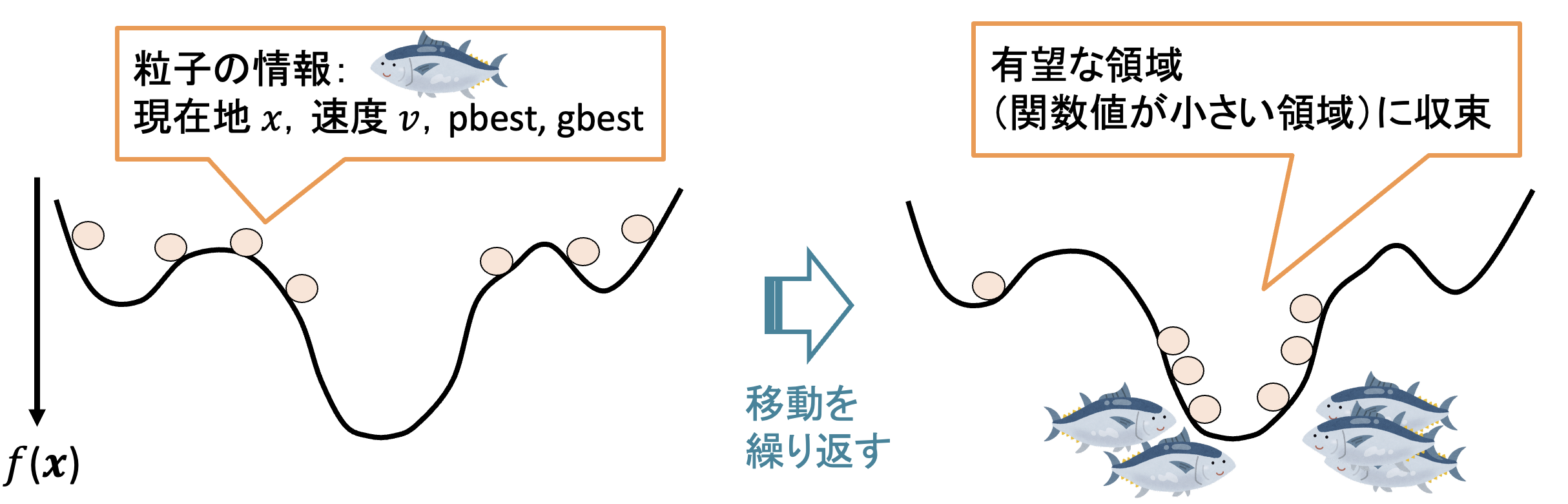
粒子群による探索のイメージ（最小化の場合）

2.2 各粒子が保持する情報

PSOにおける「粒子🐟」とは, 最適化問題の解空間における個々の解候補を指します. これらの粒子は, 解空間を飛び回りながら, 他の粒子と協力して最高の解を見つけ出すことを目指します.

粒子の構成要素

各粒子は以下の重要な情報を保持します：

位置ベクトル $\boldsymbol{x}$（Position Vector）

解空間における粒子の現在の座標であり，最適化問題の特定の解候補を表します．

速度ベクトル $\boldsymbol{v}$（Velocity Vector）

次のステップでの移動方向と速さを示し，粒子の探索方向を決定する重要な要素となります．

個体最良位置 $\boldsymbol{pbest}$（Personal Best Position）

その粒子自身がこれまでに発見した最良位置であり，粒子の「記憶」として機能します．

群全体最良位置 $\boldsymbol{gbest}$（Global Best Position）

群れ全体で発見された最良位置（最も良いpbestがgbest）であり，全粒子間で共有される情報です．

各粒子は, 自身の過去の探索経験（pbest）と, 群れ全体の探索結果（gbest）という二つの情報を利用して, 自身の位置を更新していきます.

2.3 PSOアルゴリズムの全体像

PSOの本質的な強みは, 粒子群による多点探索にあります. 単一の探索点ではなく, 複数の粒子が同時に異なる領域を探索することで, 解空間を効率的にカバーします. この集団探索アプローチにより, 個々の粒子が単独では到達できない解を, 群れ全体の協調によって発見することが可能となります.

初期状態では粒子は解空間に広く分散していますが, 移動を繰り返すことで, 粒子群は関数値が小さい有望な領域に向かって徐々に収束し, 最適解が存在する谷（最小値）に集まっていきます.

PSO処理手順のフローチャート

以下は, PSOアルゴリズムの基本的な処理手順を示しています. 初期化から始まり, 評価・更新・移動のループを繰り返し, 最終的に最適解を出力する流れとなっています.

%%{init: {'theme':'default', 'themeVariables': { 'fontSize': '36px'}}}%% flowchart LR %% ループ本体（左カラム：縦方向） subgraph loop["繰り返し処理"] direction TB S["速度
更新"] --> X["位置更新と
f(x)の計算"] X --> P["pbest
（個体最良）
更新"] P --> G["gbest
（全体最良）
更新"] G --> E{"終了判定
最大ステップ数に
達したか?"} E -- No --> T["ステップ更新
t ← t+1"] T --> S end %% 右カラム：初期化と最終出力 subgraph side[" "] direction TB INIT["初期化
粒子群を
ランダムに
生成"] OUT["最終的な
gbest
（全体最良）を出力"] end style side fill:transparent,stroke:transparent %% ループの入出力（外部接続） INIT --> S E -- Yes --> OUT %% スタイル定義 classDef thin stroke-width:2px,stroke:#333,fill:#eef4ff; classDef decision stroke-width:2px,stroke:#333,fill:#fff2a8; classDef out stroke-width:2px,stroke:#333,fill:#9f9; classDef init stroke-width:2px,stroke:#333,fill:#f9f; class S,X,P,G thin class E decision class OUT out class INIT init

フローチャートの各処理の説明

初期化：すべての粒子の位置ベクトル $\boldsymbol{x}_i$ と速度ベクトル $\boldsymbol{v}_i$ を解空間内でランダムに設定する．各粒子は異なる位置から探索を開始する．
速度の更新：各粒子の速度 $\boldsymbol{v}_i$ を更新式に従って計算する．慣性項・認知項・社会項を合成し，次の移動方向と速さを決める．
位置更新と評価：更新後の速度を用いて位置 $\boldsymbol{x}_i$ を更新し，その位置で目的関数値 $f(\boldsymbol{x}_i)$ を計算する．
pbestの更新：粒子ごとに，現在の評価値が過去の個体最良値より良ければ，個体最良位置 $pbest_i$ を現在位置に更新する．
gbestの更新：全粒子の $pbest$ のうち最良のものを $gbest$ として更新する．
終了判定：最大ステップ数に達したか，または所定の収束基準を満たしたかを判定する．
継続時のステップ更新（No の場合）：ステップ数を更新 $t \leftarrow t+1$ し，速度更新へ戻ってループを継続する．
最適解の出力（Yes の場合）：$gbest$ を最適化問題の解として出力する．

2.4 速度と位置の更新メカニズム

情報共有と収束メカニズム

PSOの探索プロセスは, 各粒子が自身のpbestと群れのgbestという2つの情報を参考にしながら, 自身の速度を更新し, 新たな位置へと移動することを繰り返すことで進行します. この情報共有メカニズムは, アルゴリズムのロバスト性（堅牢性）に大きく寄与します. 粒子は, 自身の過去の成功体験（pbest）から学び, 同時に群れ全体の最も優れた発見（gbest）からも学びます.

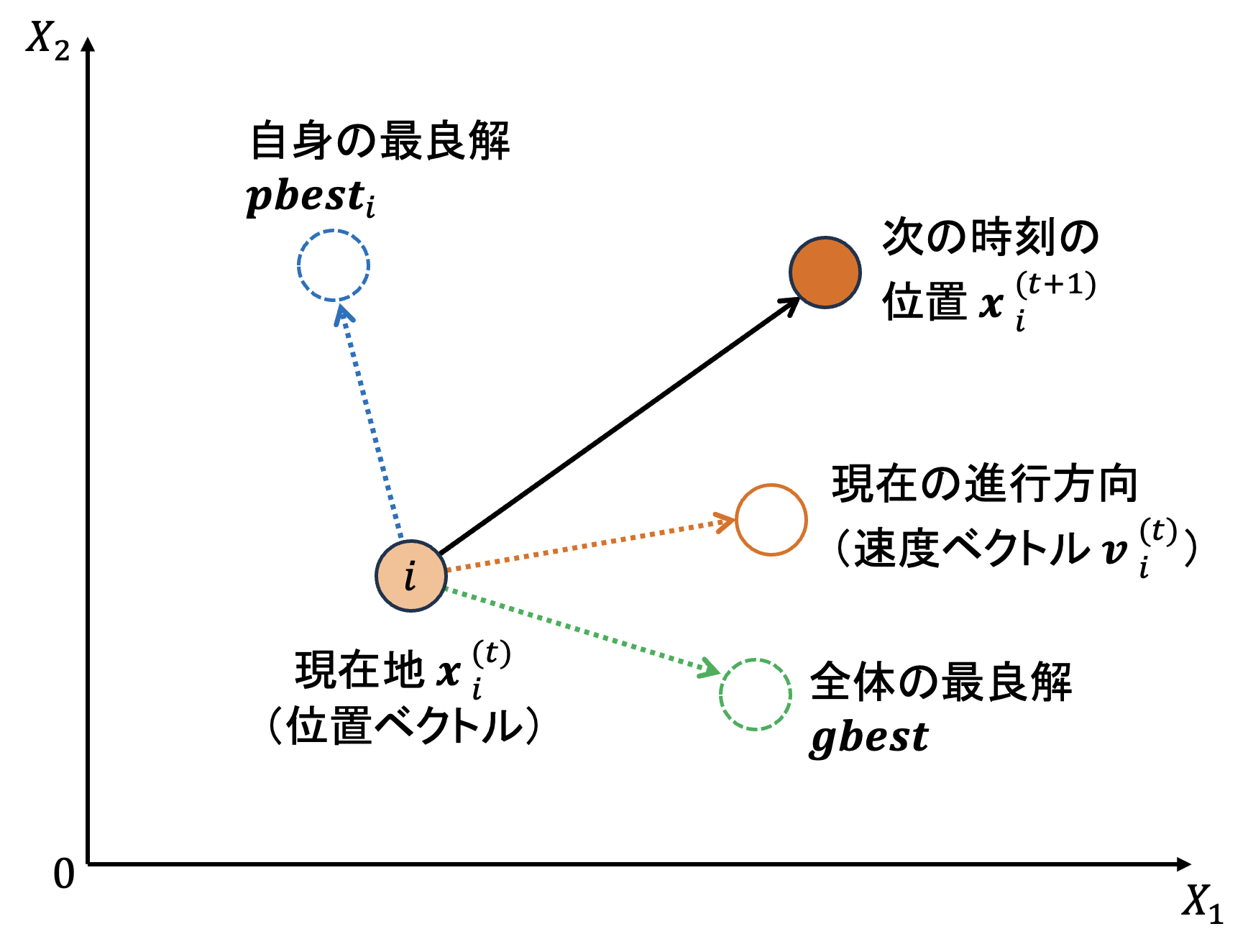
粒子の位置更新（2次元の探索空間を想定）

特に, gbestへの依存は, 仮に個々の粒子が局所的な最適解に陥ったとしても, 群れ全体の情報がその粒子をより有望な探索領域へと引き寄せることを可能にします. これにより, PSOは単一の探索者が陥りがちな局所最適解に囚われるリスクを軽減し, より広範囲にわたる探索を通じて大域的な最適解を見つけ出す能力を高めます. この集団的な学習と協調行動は, 分散型知能システムにおける, シンプルで局所的な相互作用が複雑で効果的な全体行動を生み出すという強力な原則を示しています.

速度と位置の更新式

PSOにおける粒子の動きは, 以下の速度更新式と位置更新式によって決定されます. これらの式は, 粒子の慣性, 自己認識（認知）, そして社会的な影響を数学的にモデル化し, 探索プロセスを駆動します.

速度更新式: 粒子 $i$ の次のステップでの速度ベクトル $\boldsymbol{v}_i^{(t+1)}$ は, 以下の3つの要素の合計によって決まります.
$$\displaystyle \boldsymbol{v}_i^{(t+1)} = \omega \cdot \boldsymbol{v}_i^{(t)} + c_1 \cdot r_1 \cdot (\boldsymbol{pbest}_i^{(t)} - \boldsymbol{x}_i^{(t)}) + c_2 \cdot r_2 \cdot (\boldsymbol{gbest}^{(t)} - \boldsymbol{x}_i^{(t)}) \tag{1} $$
ここで,
- $\boldsymbol{v}_i^{(t+1)}$：次の時刻における粒子 $i$ の速度ベクトル
- $\boldsymbol{v}_i^{(t)}$：現在の粒子 $i$ の速度ベクトル
- $\boldsymbol{x}_i^{(t)}$：現在の粒子 $i$ の位置ベクトル
- $\boldsymbol{pbest}_i^{(t)}$：粒子 $i$ の個体最良位置
- $\boldsymbol{gbest}^{(t)}$：群全体の最良位置
- $\omega$：慣性重み（通常0.4〜0.9）
- $c_1, c_2$：認知係数と社会係数（通常2.0）
- $r_1, r_2$：$[0,1]$の一様乱数
この式は3つのベクトルの合成によって新しい速度ベクトルを生成します. 重要なのは, これらが単なる数値の足し算ではなく, 多次元空間におけるベクトルの加算であることです. 例えば, 2次元空間では各項が$(x方向, y方向)$の成分を持ち, 3次元では$(x, y, z)$の成分を持ちます.

式(1)では, 以下の3つのベクトル成分が合成されます:
- 慣性項（慣性ベクトル） $\omega \cdot \boldsymbol{v}_i^{(t)}$: 粒子の以前の速度ベクトルをスケーリングしたもの. 現在の移動方向と速さを維持しようとする力を表現. $\omega$が大きいほど, 粒子は現在の移動方向を維持しようとする傾向が強まり, 探索空間を広く「探索」する能力が高まります.
- 認知項（個体学習ベクトル） $c_1 \cdot r_1 \cdot (\boldsymbol{pbest}_i^{(t)} - \boldsymbol{x}_i^{(t)})$: 現在位置からpbestへ向かう方向ベクトルに係数を掛けたもの. 粒子が自身の過去の成功体験から学び, 個体最良位置へ向かおうとする「自己認識」の側面を表します.
- 社会項（社会学習ベクトル） $c_2 \cdot r_2 \cdot (\boldsymbol{gbest}^{(t)} - \boldsymbol{x}_i^{(t)})$: 現在位置からgbestへ向かう方向ベクトルに係数を掛けたもの. 粒子が群れ全体の知見から学び, 全体最良位置へ向かおうとする「社会認識」の側面を表します.
これら3つのベクトルをベクトル加算することで, 粒子の次の移動方向と速さが決定されます. 各ベクトルの大きさと方向が異なるため, その合成結果は3つの力のバランスを反映した新しい方向を指し示します.
位置更新式: $$\displaystyle \boldsymbol{x}_i^{(t+1)} = \boldsymbol{x}_i^{(t)} + \boldsymbol{v}_i^{(t+1)} \tag{2} $$
- $\boldsymbol{x}_i^{(t+1)}$: 次のステップにおける粒子 $i$ の位置ベクトル. 現在の位置ベクトルに, 更新された速度ベクトルを加算することで決定されます.

PSOの主要パラメータとその役割

PSOのアルゴリズムを構成する主要なパラメータは, 探索挙動に直接的な影響を与え, 探索と開拓のバランスを制御します.

パラメータ名	記号	役割と特徴	一般的な推奨値/範囲
粒子数	$N$	群れを構成する粒子の個数. 多いほど探索範囲が広がるが, 計算コストも増大する. 問題の次元数に応じて調整が必要.	20〜50（標準）, 次元数$D$×2〜10
慣性重み	$\omega$	過去の速度をどの程度維持するかを決定. 高い値は広範囲の探索（exploration）を促進し, 低い値は局所的な探索（exploitation）を促進する. 動的に変化させる手法もある.	0.9→0.4（線形減少）または0.7〜0.9（固定）
認知係数	$c_1$	粒子が自身の最良位置（pbest）に向かう影響度を調整. 個体の自己認識と過去の成功体験への固執度合いを表す.	2.0（標準値）または1.49445
社会係数	$c_2$	粒子が群全体の最良位置（gbest）に向かう影響度を調整. 群れ全体の知見への依存度合いを表す.	2.0（標準値）または1.49445

これらのパラメータの適切な設定は, PSOの探索性能に大きく影響します. パラメータ調整は, アルゴリズムの探索挙動を精密に制御するための重要な手段となります.

例えば, 慣性重み$\omega$を高く設定すると, 粒子は自身の現在の運動方向をより強く維持し, 解空間のより広範囲を探索する傾向が強まります. 逆に$\omega$を低くすると, 粒子はpbestやgbestにより強く引き寄せられ, 既知の有望な領域を詳細に開拓する傾向が強まります.

また, 認知係数$c_1$と社会係数$c_2$の相対的な値は, 個体の自己学習と群れ全体の学習のどちらを重視するかを決定します. このように, パラメータを調整することで, ユーザはは探索と開拓のバランスを問題の特性に合わせて最適化することができます. このパラメータへの依存性は, PSOの性能を最大限に引き出すための重要な要素であり, 適応的パラメータ制御などの研究領域も存在します.

3 PSOインタラクティブシミュレータ

PSOの動作を視覚的に理解するため, インタラクティブなWebシミュレータを用意しています. このシミュレータでは, 粒子群が最適解を探索する様子をリアルタイムで観察できます.

📊 PSOシミュレータのリンク

シミュレータの特徴

リアルタイム可視化: 粒子群の動きと目的関数の等高線を同時表示
パラメータ調整: 慣性重み（$\omega$）, 認知係数（$c_1$）, 社会係数（$c_2$）をスライダーで調整可能
複数の目的関数: Sphere関数, Rastrigin関数など, 異なる特性を持つ関数で実験可能
探索履歴の表示: pbest（個体最良）とgbest（全体最良）の更新過程を追跡

このシミュレータを使うことで, パラメータの変更が粒子の挙動にどのような影響を与えるか, 直感的に理解することができます. 特に初学者の方は, まずシミュレータを動かしてみることをお勧めします.

4. PSOの特性, 強み, および限界

4.1 PSOの利点

PSOは, その設計思想とアルゴリズム構造から, 多様な最適化問題に対していくつかの顕著な利点を提供します.

計算効率の良さ: PSOは, 他の多くのメタヒューリスティック手法に比べて計算が比較的軽く, 大規模な問題に対しても迅速に解を探索できる特徴を持ちます. アルゴリズムの更新式がシンプルであるため, 初期値の設定や実装が比較的容易であり, 開発・実装コストが低いという実用的な利点も挙げられます.
局所最適解に陥りにくい: 粒子間の情報共有メカニズム, 特に群全体の最良位置（gbest）の参照を通じて, 粒子が広範囲に探索を行うため, 単一の探索者が陥りがちな局所最適解に囚われるリスクを減少させ, より良い（大域的な）解を発見しやすいという特性があります.
パラメータ調整の容易さ: PSOは, 調整すべきパラメータが比較的少なく, その意味も直感的に理解しやすいため, 特に最適化アルゴリズムの初心者でも扱いやすいという特徴があります. これにより, アルゴリズムの適用障壁が低く, 幅広い研究者や実務家によって利用されています.
非連続関数への適用性: 目的関数が非連続であったり, 微分不可能であったりする場合でも, PSOは勾配情報に依存しないため, 適用可能であるという大きな利点があります. これにより, 従来の勾配ベースの最適化手法では困難であった幅広い種類の複雑な最適化問題に対応できます.

4.2 PSOの課題

一方で, PSOにはいくつかの課題も存在し, その適用や研究においてはこれらの限界を認識することが重要です.

収束速度の遅さ: 特に非常に複雑な問題や高次元の探索空間において, 最適解に収束するまでの速度が遅くなることがあります. これは, 個々の粒子が最適な位置を見つけるのに時間がかかるためであり, 実時間性が求められるアプリケーションでは課題となる場合があります.
パラメータ依存性: PSOの探索性能は, 慣性重み（$\omega$）や加速係数（$c_1, c_2$）などの制御パラメータ設定に大きく依存します. これらのパラメータが適切でない場合, 期待した性能が得られないだけでなく, 探索が非効率になったり, 局所解に陥りやすくなったりする可能性があります. 適切なパラメータ設定は問題によって異なるため, 事前の試行錯誤やチューニングが重要となります.
局所解に陥るリスク: どの最適化アルゴリズムにも共通する課題ですが, PSOでも問題の特性や初期配置によっては, 探索が停滞し, 真の最適解に到達できずに局所解に陥る可能性は避けられません. これは, 特に多峰性の目的関数を持つ問題で顕著になることがあります.
理論的解析の難しさ: PSOアルゴリズムの確率的な挙動や, 特定の条件下での最適性に関する厳密な理論的解析は難しいとされています特定の側面（例：力学系理論に基づく決定論的PSOの解析）に焦点を当てた研究は存在するものの, アルゴリズム全体の包括的な理論的保証は依然として困難な課題であり, これが学術的な厳密性を求める研究者にとっての障壁となることがあります.

これらの利点と課題は, PSOの実用性と理論的厳密性の間のトレードオフを示しています. PSOは, その実装の容易さと複雑な問題に対する効果的な探索能力から, 多くの実世界の問題で採用されています. しかし, その一方で, 厳密な理論的保証が困難であることや, 特定の条件下での収束速度に課題があるという側面も持ち合わせています. この特性は, PSOが, 厳密解を求めることが困難な問題に対して**「十分良い」近似解を効率的に見つけ出すための強力なヒューリスティック手法として位置づけられる理由を説明します. このバランスは, ハイブリッドアルゴリズムの開発や, より適応的なパラメータ制御手法の研究を促進する要因ともなっています.

5. PSOの主要な応用分野

5.1 工学分野における最適化問題

工学分野において最適化は非常に重要な要素であり, PSOは, 厳密な解を求めるのが難しい, あるいは計算コストが非常に高い問題に対して特に有効です. その応用範囲は広範であり, 以下のような具体的な問題が挙げられます.

制御パラメータの最適化: 制御対象における時間変化する制御パラメータの最適化に利用されます. 例えば, ロボットアームの軌道計画や, 産業プロセスのリアルタイム制御などに応用されます.
有制約最適化問題: 特定の制約条件下で最適な解を見つける問題に適用されます. 日本機械学会論文集でも, 有制約最適化問題を対象としたPSOの研究が提案されています.
構造最適化: 建築物や機械部品の設計において, 材料の強度, 重量, コストなどの制約を満たしつつ最適な形状や寸法を決定する問題に利用されます. 特にトラス構造などの設計最適化に適用例があります.
組合せ最適化問題: 巡回セールスマン問題（Traveling Salesman Problem, TSP）のように, 離散的な選択肢の中から最適な組み合わせを見つける問題の解法としても研究されています.
生産スケジューリング問題: 生産システムや物流システムにおいて, 複数のタスクや資源の最適な割り当てや順序を決定し, 生産性向上に寄与します.

5.2 機械学習におけるハイパーパラメータ調整

近年, 機械学習, 特に深層学習や生成AIの分野の発展に伴い, PSOの重要性が再評価されています. これらの機械学習モデルのトレーニングプロセスでは, 学習率, バッチサイズ, ネットワーク構造, 正則化係数など, 数多くのハイパーパラメータが複雑に絡み合います. これらのパラメータの最適な組み合わせを見つけることが, モデルの性能を大きく向上させる鍵となります.

PSOは, 機械学習モデルの効率的なハイパーパラメータ最適化に活用されます. その計算効率の良さ, 実装の容易さ, そして目的関数が非連続であったり微分不可能であったりする場合でも適用可能であるという特性は, 複雑なハイパーパラメータ空間を探索する上で非常に有利です. これにより, 手動での試行錯誤に比べて, より短時間で高性能なAIモデルを構築することが可能になります.

さらに, 画像処理や音声認識といった特定の機械学習タスクにおけるパラメータ調整にもPSOが応用されています. これは, 現代の機械学習モデルが抱える「最適な設定を見つける」という課題に対して, PSOが実用的な解決策を提供できることを示しています. この応用領域の拡大は, PSOが単なる古典的な最適化アルゴリズムに留まらず, 最先端の人工知能研究と開発においてもその価値を維持し, 進化し続けていることを明確に示しています.

5.3 その他の応用例

PSOの普遍的な最適化能力は, 上記の分野以外にも多岐にわたる領域で活用されています.

医学・生物学分野: ゲノム・遺伝子解析アルゴリズムの研究や, 複雑な医学的・生物学的現象のモデリングとデータへのフィッティングに利用されます. 例えば, 薬剤設計における分子構造の最適化や, 生物学的システムのパラメータ推定などに適用されます.
経済学分野: 経済学的な現象をモデル化し, 大量のデータにフィッティングさせる問題に適用されます. 特に, 変数の数が1万から100万にも及ぶような大規模な経済モデルの最適化において, PSOは強力なツールとなり得ます.
小型群ロボットの開発: 計算機シミュレーションだけでなく, 実際の小型群ロボットの開発において, 群れの振る舞いの確認や, その特性を活かした応用・使用方法の検討が進められています. これは, 群知能アルゴリズムがシミュレーションの世界から現実世界へと展開され, 物理的なシステム制御に応用される可能性を示しています.

これらの多様な応用例は, PSOが, 高次元, 複雑, あるいは非線形な探索空間において最適な解を見つけるという普遍的な課題に対して, 強力な解決能力を持つことを示しています. 従来の解析的または勾配ベースの手法が適用困難な場合に, PSOは効果的な代替手段を提供し, 様々な分野における意思決定や設計プロセスの最適化に貢献しています.

参考文献

研究報告

捕食者を加えた粒子群最適化での捕食範囲の調査 - 徳島大学, 最終アクセス：2025/8/9, http://nlab.ee.tokushima-u.ac.jp/nishio/Pub-Data/WORK/W572.pdf
粒子群最適化を用いた巡回セールスマン問題の解法 - IEICE, 最終アクセス：2025/8/9, https://www.ieice.org/publications/conference-FIT-DVDs/FIT2019/data/pdf/A-005.pdf
力学系理論に基づく粒子群最適化法の解析 - J-Stage, 最終アクセス：2025/8/9, https://www.jstage.jst.go.jp/article/essfr/15/2/15_70/_article/-char/ja
衝突を伴う確定的粒子群最適化法 - IEICE, 最終アクセス：2025/8/9, https://www.ieice.org/publications/conference-FIT-DVDs/FIT2013/data/pdf/F-029.pdf
粒子群最適化による現場計測データを用いたトンネル逆解析 - 西松建設, 最終アクセス：2025/8/9, https://www.nishimatsu.co.jp/solution/report/pdf/vol36/g036_12.pdf
構造最適化問題における粒子群最適化法の探索性能について - 日本建築学会, 最終アクセス：2025/8/9, http://news-sv.aij.or.jp/jyoho/s1/proceedings/2013/pdf/H59.pdf
有制約最適化問題を対象とした粒子群最適化の一提案（第１報：ベンチマーク問題を用いた基礎的検討） - J-Stage, 最終アクセス：2025/8/9, https://www.jstage.jst.go.jp/article/transjsme/advpub/0/advpub_24-00262/_article/-char/ja/

大学・研究機関等の公開資料

Particle Swarm Optimization(PSO)とは - 伊庭研究室 - 東京大学, 最終アクセス：2025/8/9, http://www.iba.t.u-tokyo.ac.jp/software/PSO_Simulator.html
生き物の進化から学び, 科学技術の発展を加速する. | 研究室紹介 | TELESCOPE magazine, 最終アクセス：2025/8/9, https://www.tel.co.jp/museum/magazine/020/lab01/
用語解説第44回テーマ：粒子群最適化(PSO) ～生物の採餌行動を模擬した最適化手法, 最終アクセス：2025/8/9, https://www.iee.jp/pes/termb_044/
人工知能 - 粒子群最適化 - Microsoft Learn, 最終アクセス：2025/8/9, https://learn.microsoft.com/ja-jp/archive/msdn-magazine/2011/august/artificial-intelligence-particle-swarm-optimization
粒子群最適化（Particle Swarm Optimization） - サイバネットシステム, 最終アクセス：2025/8/9, https://www.cybernet.co.jp/noesis/column_glossary/glossary/particle_optimization/